| автор Джон Тэйлор
Главы:
[2]
Глава 2. Оттянутая струна
2.1 Потребность в теоретической модели
В этой и следующей главах будет сделана попытка выделить физические принципы, которые управляют способами извлечения звука на гитаре. Эти принципы определяются поведением двух связанных вибраторов гитары … струн и корпуса. К сожалению, последний все еще сравнительно мало изучен с точки зрения акустики, частично потому что индивидуальные гитары отличаются друг от друга многими деталями, а также потому что гитара еще не подвергалась обширному научному исследованию, в отличие от смычковых струнных инструментов и фортепиано. Но благодаря, главным образом, работе, проделанной на указанных инструментах, многое известно о натянутых струнах вообще. Поэтому наше внимание в этой главе будет сфокусировано непосредственно на поведении струны, и мы найдем, что многие (но ни в коем случае не все) из способов извлечения различных звуков на гитаре могут быть поняты таким способом, без погружения в детали взаимодействия струны и корпуса.
Даже когда это взаимодействие игнорируется, движение оттянутой струны достаточно трудно описать точно. Струна имеет некоторую жесткость; ее колебания заглушаются внутренним трением и сопротивлением воздуха; ее эффективная длина может изменяться из-за перемещения концевых опор струны. Сталкиваясь со сложностями такого рода, физик обычно не пытается включить их всех в один огромный расчет. Вместо этого он обращается к теоретической модели, поведение которой легче понять, а затем смотрит, можно ли изменить или расширить эту модель, чтобы включить различные факторы, которые он сначала отбросил. Это было проделано, с некоторым успехом, для оттянутых струн1. Действительно, если пренебречь упомянутыми выше сложностями, оттянутая струна … простейшая из всех колебательных систем, и любима математиками, так как ее движение допускает точный анализ. Предполагается, что струна совершенно гибкая и однородная, не подвергается никакому демпфированию любого вида, и неподвижно зафиксирована на каждом конце. Несмотря на то, что в реальности подобной струны никогда не существовало, с помощью этой модели можно узнать поразительно много. С ее помощью мы получим многие из идей этой главы; но, так как эта книга направлена в основном на практику, то по ходу рассуждений мы без малейших сомнений будем отступать от идеализированной теории, чтобы сделать выводы, касающиеся техники игры на реальных струнах.
2.2 Основная частота натянутой струны.
Некоторые из читателей могут быть знакомы со школьным экспериментом с наиболее немузыкальным инструментом, сонометром, в котором показано, что частота колебаний натянутой струны зависит только от ее колеблющейся длины l, ее натяжения (то есть растягивающего усилия) T и ее массы на единицу длины m. К счастью, нет никакой необходимости описывать этот эксперимент здесь, но результат (который также можно получить математически из простой модели), стоит знать:
Основная частота 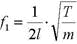
Эти формула показывает, что частота увеличивается пропорционально уменьшению длины, или пропорционально увеличению квадратного корня натяжения, или пропорционально уменьшению квадратного корня линейной плотности. Таким образом, деление длины напополам удваивает частоту и повышает высоту звука на октаву … что хорошо всем известно, так как двенадцатый лад лежит посередине между нижним и верхним порожком. С другой стороны, чтобы поднять высоту звука на октаву, натяжение струны необходимо увеличить в четыре раза. Это говорит о том, что настраивать струны значительно выше рекомендуемой высоты звучания … плохая идея: например, повышение настройки всех струн на тон увеличит нагрузку на нижний порожек и непосредственно на сами струны на 26%. Усилие натяжения струны, настроенной по присущей ей высоте звучания таким же образом зависит от мензуры инструмента.
При одинаковой мензуре надлежащее натяжение пропорционально линейной плотности струны. Другими словами, струны высокого натяжения … это тяжелые струны, струны низкого напряжения … легкие струны. Однако в пределах комплекта струн натяжение значительно изменяется от струны к струне. Если все три дискантовые струны сделаны из одного материала … нейлона, то третья струна должна иметь значительно меньшее натяжение, чем первая, чтобы избежать чрезмерной толщины. По той же самой причине басовые струны сделаны из волокон нейлона c оплеткой из металлической нити, которая добавляет вес, не увеличивая при этом слишком сильно толщину и жесткость. Четвертая струна, будучи первой из струн с металлической оплеткой, обычно имеет намного более высокое натяжение, чем третья, и немного более высокое натяжение, чем две самые низкие.
2.3 Техника вибрато
Натяжение струны непосредственно влияет на звукоизвлечение, по крайней мере, в одном отношении: на гитаре, все вибрато выполняются посредством изменения натяжения, так как колеблющаяся длина струны определяется ладом. Поэтому перекатывание кончиков пальцев левой руки, используемое для создания вибрато исполнителями на инструментах семейства скрипки, которое изменяет колеблющуюся длину струны, на гитаре будет неэффективным. Вместо этого вибрато обычно исполняется путем плотного прижатия кончика пальца к струне и перемещения кисти руки вверх-вниз вдоль струны, что позволяет повышать и понижать натяжение колеблющейся части струны.
Важно понять, что при этом также изменяется и натяжение в неподвижной части струны между пальцем и верхним порожком. При игре на двенадцатом ладу, усилия разделяются одинаково между двумя частями струны, но в более низких позициях неподвижная часть отнимает больше усилий. На пятом ладу, например, только четверть приложенного усилия фактически идет на изменение натяжения в колеблющейся части струны, в то время как на первом ладу, все, кроме приблизительно одной восемнадцатой приложенного усилия тратится впустую.
Фактически весьма трудно добиться заметного вибрато нормальным способом ниже четвертого лада, и в этой области грифа часто вместо обычного вибрато используется боковое вибрато. Оно заключается в попеременном отведении струны в сторону, перпендикулярно направлению ее длины, приближая кончик пальца к ладони руки, и возвращая его в исходное положение. (Так как перемещение струны или только к ладони или только от нее дает небольшое увеличение натяжения, некоторые авторы рекомендуют совершать оба движения. Это более аккуратно и удобно, чем подтяжка только в одном направлении). Боковое вибрато может использоваться в любом месте струны, но около своей середины струна слишком гибкая. Кроме того, при боковом вибрато высота ноты только повышается относительно исходной, поэтому в целом нота звучит слегка повышенно. В большинстве случаев нормальным вибрато легче управлять и оно вполне удовлетворительно.
Мы видим, что нормальное вибрато требует тем меньшего усилия, чем выше номер лада. По той же самой причине, хорошее интонирование требует все большего внимания в более высоких позициях. В первой позиции можно изменять натяжение струны более или менее безнаказанно, но выше двенадцатого лада любая струна при таком же воздействии будет звучать ужасно.
Наконец, стоит заметить, что изменения высоты, которые происходят при исполнении вибрато, пропорциональны относительным изменениям натяжения струны. Следовательно, слабее натянутые струны более чувствительны к вибрато, чем более натянутые; и, напротив, на них труднее получить звук нужной высоты (интонировать). То же самое, при прочих равных, относится и к гитарам с меньшей мензурой.
2.4 Формы колебаний струны
Как известно, звучание ноты, извлеченной на гитаре, в значительной степени зависит от того, где и как она была извлечена. В разделе 1.3 мы узнали, что тембр звука определяется совокупностью обертонов, или одночастотных компонентов, присутствующих в форме звуковой волны. Если принять это во внимание, то не должен вызывать удивления тот факт, что струну можно рассматривать как колеблющуюся с несколькими частотами одновременно. В случае струны, которую защипнули и оставили свободно колебаться, это собственные частоты струны.
Одним из способов определения этих собственных частот заключается в вынуждении струны колебаться с какой-либо одной частотой и наблюдении за откликом струны по мере изменения частоты. Например, можно поместить стальную струну или нейлоновую струну с металлической обмоткой между полюсами магнита и пропустить через струну ток (соответствующим образом усиленный) от генератора синусоидальной волны. Предположим, что струна настроена в Ля, частота 110 Гц. При частотах намного ниже этой отклик струны сравнительно слаб, но в непосредственной окрестности 110 Гц амплитуда колебаний внезапно значительно возрастает. Говорят, что струна резонирует на частоте 110 Гц, форма возникающих при этом колебаний показана на Рис. 2.1(a). (Два крайних положения колебательного движения показаны непрерывной и штриховой линиями.) Это первая, или основная, форма колебаний, и сильнее всего она возбуждается усилием, приложенным в середине струны, там, где эта форма имеет петлю.
Рис. 2.1 Формы колебаний струны, настроенной в Ля (110 Гц)
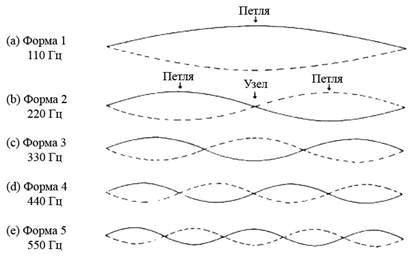
Если частоту вынуждающего усилия увеличить сверх 110 Гц, то отклик мгновенно уменьшиться, но на частоте 220 Гц резонанс возникнет снова. Это вторая форма, показанная на Рис. 2.1(b). Она имеет узел, или неподвижную точку, в середине и две петли; отклик будет максимальным, если вынуждающее усилие приложено в одной из двух петель, но он уменьшается до нуля в узле. Третья форма, показанная на Рис. 2.1(c), имеет частоту 330 Гц, три петли и два узла. Следующие две формы подтверждают закономерность: каждый раз при увеличении частоты на 110 Гц возникает еще один резонанс, при этом каждая следующая форма имеет на один узел и на одну петлю больше, чем предыдущая.
В реальности одним из эффектов жесткости струны является некоторое увеличение частотного расстояния между высшими формами. Однако в первом приближении частоты форм реальной струны следуют соотношению, описываемому формулой:
Частота n-ой формы = n · основная частота
Вы можете заметить, что это также является соотношением, которое должно выполняться между основной частотой и любым обертоном, добавление которого не изменит частоту повторения результирующей формы волны (см. раздел 1.3). В двух словах … это причина, почему струны являются таким полезным источником музыкальных звуков. Струна может колебаться по нескольким формам одновременно, но она все равно будет издавать музыкальный звук, поскольку ее собственные частоты соотносятся гармонически.
2.4 Гармонический ряд
Мы узнали, что последовательные формы колебаний струны равномерно распределены по частоте. Это означает, что музыкальные интервалы между ними уменьшаются по мере увеличения номера формы (см. раздел 1.2). Например, вторая форма находится на октаву выше основной, поскольку ее частота в два раза выше; однако интервал между второй и третьей формами составляет всего лишь чистую квинту, поскольку соотношение их частот составляет 3:2.
Ряд высот, соответствующих частотам последовательных форм, на самом деле хорошо знаком музыкантам как гармонический ряд. Первые десять членов ряда для основной частоты 110 Гц показаны на Рис. 2.2. В случае, если частота формы отличается от частоты приведенной ноты, последняя приведена в скобках (частота вычислена на основе темперированного звукоряда, в котором октава разбита на двенадцать равных полутонов2). Для удобства была выбрана высота открытой струны Ля, однако эта же последовательность, должным образом транспонированная, применима к любой другой ноте на гитаре. Соответствие выдерживается даже для разностей между частотами форм и ближайшими к ним нотами темперированного звукоряда, выраженными через доли полутонов.
Рис. 2.2 Высоты, соответствующие первым десяти формам открытой струны Ля

Первое существенное расхождение наблюдается в пятой форме. Если исходить из темперированного звукоряда, то высота этой формы примерно на одну восьмую полутона ниже, что составляет хотя и небольшую, но достаточно заметную разницу. По этой причине натуральный флажолет, взятый на четвертом ладу шестой струны скорее всего будет звучать ниже, чем нота соль-диез на первой струне, несмотря на то, что открытые струны настроены с интервалом точно в две октавы. (О том, что такое флажолеты, рассказывается в разделе 2.10.) Также это частично объясняет, почему третья струна, если ее точно настроить так, чтобы она давала консонансный Соль-диез в аккорде Ми мажор в первой позиции, при защипывании открытой струны дает слегка пониженную ноту Соль в аккорде До мажор; другая причина заключается в том, что нейлоновая третья струна настолько чувствительна к изменениям натяжения, что даже простое прижимание ее на первом ладу может немного повысить ноту.
Разница для седьмой формы колебаний настолько велика (примерно одна треть полутона), что уже нельзя сказать, что высота звука, производимого этой формой, принадлежит нашей западной музыкальной системе. Также эта форма является первым членом последовательности, образующей диссонансные интервалы с основной формой и со своими ближайшими соседями. Скорее всего по этой причине звук, богатый высшими обертонами, имеет резкий характер, его «жесткость» связана, в частности, с теми обертонами, которые выше основного тона по крайней мере на три октавы.
2.6 Возбуждение форм колебаний защипыванием
В разделе 2.4 мы рассматривали отклик струны на воздействие переменной силы, имеющей одну частоту. Можно представить более подробный эксперимент, в котором приложенная сила содержит несколько компонентов с различными частотами, каждая из которых соответствует одной из форм колебаний струны. Струна будет колебаться по всем этим формам одновременно, причем сила возбуждения каждой формы будет зависеть от амплитуды соответствующего компонента силы и от положения точки приложения силы на струне. Например, если силу приложить в точке, отстоящей от конца струны на четверть длины, то наибольшее возбуждение, вызванное усилием, будет для формы 2 (которая имеет в этой точке петлю), а для формы 4 (имеющей в этой точке узел) возбуждение будет нулевым. Вообще, более низкие формы будут сильнее возбуждаться силой, приложенной ближе к середине струны, а высшие формы … усилием, приложенным возле одного из концов.
Однако более простым способом заставить струну колебаться сразу по нескольким формам является обыкновенное защипывание. Общие замечания, сделанные в предыдущем абзаце, в той же мере относятся и к данному случаю, но особенно полезным для точного вычисления амплитуд каждой формы будет использовать модель идеальной струны, если нам известна форма струны перед высвобождением. Если идеальную струну оттянуть в сторону в точке, отстоящей от одного из концов на некоторое относительное расстояние (назовем его p) и отпустить, то в результате анализа мы придем к изящной формуле3, позволяющей получить амплитуду любой формы колебаний, зная p и ее номер n.
Совсем необязательно углубляться в математику, чтобы визуально представить себе, как работает это преобразование Фурье. (Мы уже видели пример этого же принципа, когда рассматривал синтез пилообразной волны.) Форма струны перед высвобождением рассматривается как сумма синусоидальных кривых, соответствующих различным формам колебаний, показанным на Рис. 2.1. В реальности струна удерживается, а после высвобождения будет колебаться по форме, в точности соответствующей сумме синусоид, необходимых для получения начальной формы.
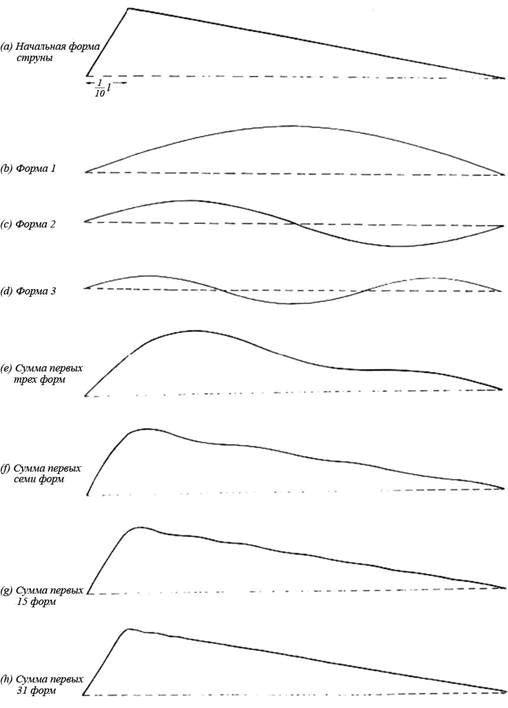
Пример такого синтеза для струны, защипываемой на расстоянии в одну десятую длины (p = 1/10), показан на Рис. 2.3. Сверху показана форма струны, которую необходимо получить, причем поперечные отклонения преувеличены для улучшения восприятия. Ниже показаны три первые формы, каждая со своей амплитудой. Кривая (e) является результатом сложения перемещений этих трех форм; на этой стадии треугольная форма уже начинает вырисовываться, но очевидно, что, для того, чтобы приблизиться к прямым линиям и достаточно острому углу начальной формы, придется проделать еще много операций. Если сюда добавить еще формы с 4 по 7 (которые находятся в третьей по счету октаве от основной формы), то мы получим кривую (f), которая является более качественным приближением. Это вполне ожидаемо, так как точка защипывания находится в петле формы колебаний номер 5, и достаточно близко к ней для форм 4, 6 и 7. Общая тенденция заключается в том, что более высокие формы колебаний вносят все меньший и меньший вклад в форму кривой. Следующие восемь только слегка заостряют кривую до формы кривой (g), а формы 16-31, которые лежат в 5-й октаве, вместе дадут только легкое улучшение, показанное как кривая (h). В действительности, на этом этапе уже практически ничего нельзя сделать, чтобы улучшить совпадение форм. Также как и с синтезом пилообразной волны, потребовалось бы бесконечное число форм все меньшей амплитуды, чтобы получить идеальную форму с заострением, но такое отклонение на самом деле невозможно. Фактически число эффективных форм колебаний гитарной струны ограничивается жесткостью струны и лежит в пределах приблизительно от двадцати до сорока, что было показано в разделе 2.1.
Рис. 2.3 Синтез формы идеальной струны перед высвобождением, p = 1/10
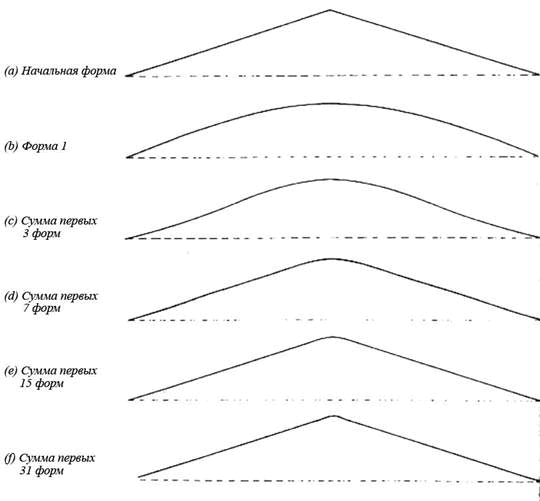
Второй пример, на этот раз для защипывания струны в центре (p = 1/2), показан на Рис. 2.4. В этом случае все четные формы отсутствуют, поскольку в этой точке они имеют узел. Что касается оставшихся форм, которые все имеют петлю в центре, то основной тон наиболее значимый из них, т.к. высшие формы очень слабо возбуждаются по сравнению с ним. Отсутствие четных форм придает звуку, взятого точно в центре струны, специфический пустой тембр, часто называемый арфообразным, кажется, только потому, что арфисты рассматривают середину струны как нормальную щипковую точку.
Рис. 2.4 Синтез формы идеальной струны перед высвобождением, р=1/2
2.7. Распределение энергии между формами
При защипывании струне сообщается энергия. Защипывание струны в разных местах меняет распределение энергии между формами. Например, энергия может направиться предпочтительно во вторую форму при защипывании в точке, отстоящей от конца на четверть длины струны, или в десятую форму при защипывании в точке, отстоящей на 1/20 длины. Общая тенденция распределения энергии показана на Рис. 2.5 понятным, пусть и немного необычным способом. Для каждого значения р (относительное расстояние до точки защипывания на струне), я вычислил соответствующие энергии, сообщаемые формам вплоть до 31-й, и сгруппировал их вместе по октавам. А именно: 1-я октава содержит только основной тон, вторая включает формы 2 и 3, третья … формы 4-7, четвертая … формы 8-15, и пятая … формы 16-31. Таким способом можно увидеть распределение энергии по всему музыкальному диапазону над основным тоном, а также можно сравнить эту диаграмму с Рис. 2.3 и 2.4, где мы применяли аналогичную группировку форм.
Рис. 2.5 Распределение энергии первых 5-ти октав для идеальной струны, защипнутой в разных точках
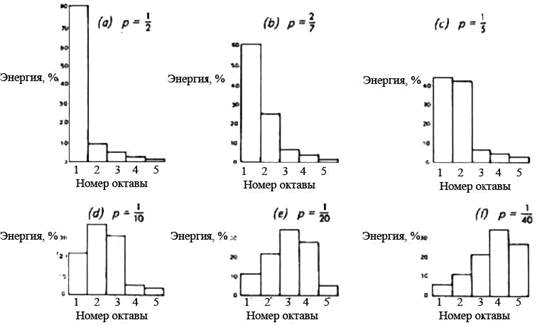
Из Рис. 2.5 видно, что если струну защипнуть в середине (р = 1/2), то почти вся энергия уходит в основной тон, оставляя меньше 20% на все остальные формы. Защипывание открытой струны выше розетки (р = 2/7) направляет часть энергии во вторую форму, но формы в трех высших октавах еще относительно слабо возбуждаются. В нормальной игровой позиции (я считаю, что это около р = 1/5) вторая и третья формы вместе получают примерно столько же энергии сколько основной тон, но для высших форм остается все еще очень мало энергии. Перемещение ближе к подставке (р = 1/10) отнимает энергию от основного тона и передает ее формам в третьей октаве; но формы в четвертой октаве в целом слабо выделены, т.к. 10 форма имеет узел в точке защипывания и, естественно, полностью исключается из звука. Однако, эти высшие формы выделяются, если точка защипывания находится возле подставки (р = 1/20), пока наконец не станут преобладать при защипывании струны максимально близко к подставке (р = 1/40).
Однако воспринимать эти схемы следует с некоторой осторожностью. Во-первых, они показывают только количество энергии, которое мы сообщаем различным формам колебаний, а в звук может быть преобразована только та энергия, которая исходит из струны. В этом отношении наша идеальная струна имеет весьма существенный недостаток: после защипывания она будет бесконечно колебаться неизменным образом, не теряя энергию ни одним из способов и не производя никакого звука! Настоящая струна теряет энергию посредством внутреннего демпфирования и, с помощью корпуса гитары, через звук. То есть, то что мы слышим, определяется главным образом откликом корпуса гитары, который может сильно различаться для разных нот, и даже для разных обертонов одной и той же ноты4.
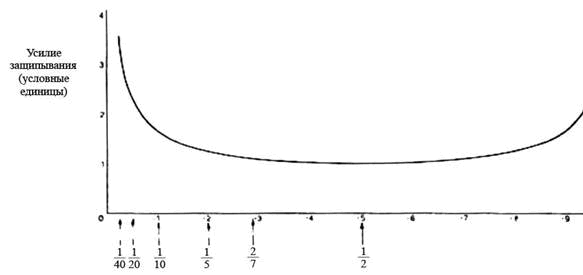
Во-вторых, схемы на Рис. с 2.5(a) по (f) можно сравнивать только между собой, так как предполагается, что в каждом случае струне сообщается одинаковое количество энергии. Чтобы достичь этого, необходимо защипывать струну вблизи конца струны с большим усилием, нежели возле середины, как следует из Рис. 2.6. Резкий рост требуемого усилия на концах струны является одной из причин того, что играть слишком близко к подставке непрактично. Играя в рамках обычного диапазона точек защипывания, примерно от 1/10 до 1/2, гитарист привыкает изменять прикладываемое усилие, и понимает, что он может приложить большее усилие при игре возле подставки (где струна ощущается более «тугой»), чем возле розетки, не опасаясь переиграть.
Рис. 2.6 Зависимость усилия защипывания, необходимого для сообщения струне одинакового усилия от положения точки защипывания
Но даже с такими ограничениями мы все равно можем почерпнуть полезную информацию из этих схем распределения энергии. Они демонстрируют, почему при защипывании струны возле подставки (p = 1/20) получается яркий и жесткий звук … яркий потому, что выделяются обертоны, лежащие в третьей и четвертой октавах от основного тона, а жесткий потому, что многие из этих обертонов диссонируют с основным тоном. Будет нелишним заметить, что если в этой точке защипнуть открытую шестую струну, то подчеркиваемые формы колебаний лежат в частотном диапазоне самых высоких нот на грифе гитары, а если в этой же точке защипнуть открытую первую струну, то подчеркиваемые формы будут лежать еще на две октавы выше, в частотном диапазоне, к которому наиболее чувствителен слух человека.
Также мы можем, с должной осторожностью, сделать некоторые общие выводы о громкости, которую можно ожидать, если защипывать струну в различных точках, воспользовавшись информацией из раздела 1.4. Громкость там рассматривалась через мощность (мера скорости передачи энергии), в то время как сейчас мы можем знать только начальную энергию каждой формы. Тем не менее, мы можем, например, увидеть, что схема для струны, защипнутой в середине, имеющая высокий пик на основной частоте, не обязательно означает, что этот звук будет более громким по сравнению с остальными схемами, пики которых имеют меньшую высоту. При p = 1/2 основная форма колебаний получает примерно в девять раз больше энергии, чем форма 3, но из этого не следует, что она будет в девять раз громче; вероятней всего, она будет звучать только примерно в два раза громче. При прочих равных равномерное распределение энергии среди всех форм даст более громкий звук, чем концентрирование энергии в одной. На практике необходимо еще учитывать отклик инструмента, а также большее усилие защипывания, необходимое возле подставки; но вообще самые громкие и выразительные звуки получаются при игре над ближним к подставке краем розетки.
Напоследок следует рассмотреть одно из следствий того, что распределение энергии зависит от относительного положения точки защипывания на струне. Гитаристы иногда исполняют мелодическую фразу на одной струне, чтобы избежать внезапных изменений тембра. Но если при переходах левой руки с одного лада на другой не изменять одновременно позицию правой руки, то при этом будет меняться относительное расстояние p, а, следовательно, и распределение энергии по формам колебаний и получающуюся окраску звука. В большинстве случаев достаточно сложно, да и не нужно постоянно менять позицию правой руки, однако если требуется идеально ровный звук, то лучше всего будет двигать обе руки вверх или вниз одновременно. Читатель может проверить, что если правая рука будет всегда двигаться в том же направлении, что и левая, но на меньшее расстояние, составляющее p от пройденного левой рукой, но значение p при защипывании не изменится.
2.8 Методы подавления высших форм колебаний
Мы подошли к концу достаточно продолжительного обсуждения эффекта защипывания струны в разных точках. Разумеется, контроль за звуком этим не исчерпывается. Звук ноты зависит не только от того где, но и от того, как защипывается струна. До настоящего момента предполагалось, что струна оттягивается за одну точку и мгновенно высвобождается. Это примерно эквивалентно использованию жесткого заостренного медиатора, который, естественно, будет извлекать жесткие, тонкие звуки. Есть два основных способа получения более мягкого звука; и тот и другой уменьшают возбуждение высших форм колебаний.
(a) Использование закругленного предмета для защипывания
Если вернуться к рисункам, демонстрирующим синтез начальной формы струны для двух разных точек защипывания (Рис. 2.3 и 2.4), то можно заметить, что в обоих случаях роль форм колебаний в высших октавах в основном сводится к улучшению формы острого угла в точке защипывания. Отсюда следует, что если струну оттягивать с помощью закругленного предмета, то высшие формы будут возбуждаться менее сильно.
Этот факт приводится в большинстве книг по общей музыкальной акустике5, и он, несомненно, полезен. Однако нижеследующий приблизительный расчет показывает, что его значение для гитаристов было, по всей видимости, переоценено. Предположим, что вместо узкого медиатора струну оттягивают кончиком пальца, используя его на всю ширину в 2 см. Можно ожидать, что таким образом буду подавлены все формы, имеющие узел на участке струны длиной 2 см. Для струны длиной 65 см это означает что будут отсутствовать все формы с номером выше примерно 32 … но этот же самый предел уже установлен жесткостью струны! Другой способ проверить это … обратить внимание на контур струны, оттянутой узким предметом. Любая нейлоновая струна слишком жесткая, чтобы образовать острый угол вокруг этого предмета, и можно увидеть, что контур струны практически не изменится, если вместо этого ее оттянуть кончиком пальца. Очевидно, что различия в начальных формах струн слишком малы, чтобы вызвать такую радикальную разницу в звуке, который получается при использовании этих двух предметов.
(b) Постепенное высвобождение струны
Важнейшим фактором, еще не рассмотренным нами, является способ, которым осуществляется высвобождение струны. Исследуем его сейчас, воспользовавшись уже известной нам упрощенной моделью. Перед высвобождением струна удерживается на месте усилием, приложенным в точке защипывания. Когда это усилие внезапно исчезает в момент высвобождения, то в этой точке возникает несбалансированное усилие, вызванное натяжением струны. В результате этого струна мгновенно приводится в движение в точке защипывания, а позже … во всех остальных точках между ее неподвижными концами.
Если рассматривать точку «заострения» струны в момент перед высвобождением как скачок в пространстве, то можно сказать, что внезапное приведение этой точки в движение … скачок во времени. Они неразрывно связаны друг с другом, и можно считать, что высшие формы колебаний возбуждаются скачками обоих типов. И наоборот, высшие формы можно подавить, сгладив либо скачок в пространстве, уменьшив остроту угла, либо скачок во времени, высвободив струну постепенно, а не мгновенно. Мы узнали, что диапазон возможностей гитариста по сглаживанию начальной формы струны ограничен небольшой по сравнению с длиной струны шириной кончика пальца. С другой стороны, время, которое кончик пальца или ноготь могут провести на струне перед ее высвобождением, ничем не ограничено.
Продемонстрируем данный принцип постепенного высвобождения струны на нескольких примерах. Предположим, что мягкий кончик пальца оттягивает струну на расстояние, равное своей толщине, как показано на Рис. 2.7(a). Если струна сейчас начнет соскальзывать по кончику, то ей сначала необходимо будет, набирая ускорение, пройти все расстояние, на которое она была оттянута, прежде чем она соскочит с кончика пальца. Это наиболее постепенное высвобождение струны, процесс в данном случае растянут на первую половину цикла движения струны. Еще немного медленнее, и кончик пальца начнет гасить колебания. На самом деле высшие формы колебаний уже будут в значительной степени подавлены, и, вероятно, это является причиной, по которой извлечение чистого или яркого звука с помощью только мясистой части пальца сильно затруднено. Если же, напротив, оттягивать струну кончиком ногтя строго поперек струны, как показано на Рис. 2.7(b), то путь струны по ногтю может быть пренебрежимо мал по сравнению с расстоянием, на которое она была оттянута, и высвобождение будет практически мгновенным. А если этот же самый ноготь разместить под углом, как на Рис. 2.7(c), то путь, который проходит струна значительно удлиняется и появляется возможность в значительной степени влиять на звук, изменяя этот угол. Однако многое зависит от формы и состояния ногтя, который во всех случаях должен обеспечивать струне гладкое прохождение, что позволит избежать резких звуков. В общем случае любая неровность начального движения струны может возбудить высшие формы колебания и придать звуку резкий характер6.
Рис. 2.7 «Постепенное» и «быстрое» высвобождение струны
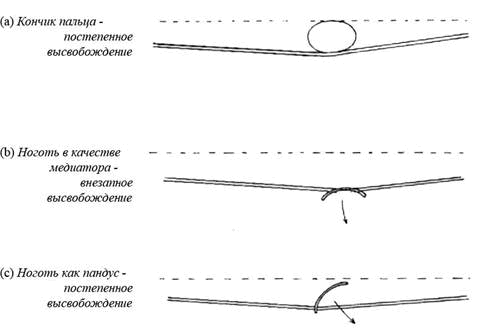
Необходимо понимать, что то, что мы называем «постепенным» высвобождением (занимающее примерно половину цикла) на самом деле происходит очень быстро по обычным меркам. Например, половина цикла открытой струны Си (247 Гц) занимает примерно две миллисекунды. Следовательно, контролировать движение струны после того, как она начала соскальзывать по кончику пальца или ногтю практически невозможно. Тем не менее, мы можем … и в этом, несомненно, заключается секрет управления звукоизвлечением … заранее проложить путь струны, поставив перед ней препятствие определенного размера, формы и структуры. Более подробно о том, как это можно сделать, будет рассказано в следующих главах. Пока можно заметить, что ноготь с хорошей формой является более универсальным средством предопределения движения струны, нежели любой кончик пальца. Ноготь можно использовать перпендикулярно струне, как медиатор, быстро высвобождая струну, или под углом, подобно пандусу, позволяя струне скользить по нему. Если ноготь представлять как пандус, то можно обнаружить еще одну крайне важную его функцию, которая будет описана в Главе 4.
2.9 Движение струны после высвобождения
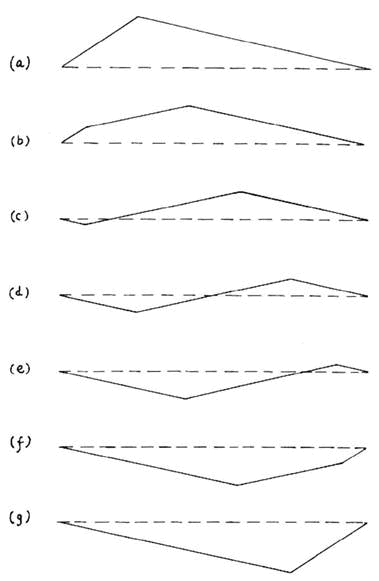
Прежде чем закончить работу с упрощенной моделью, мы можем получить с ее помощью еще одну полезную идею. После высвобождения идеальная струна колеблется полностью предсказуемым и повторяющимся образом. Это движение показано на Рис. 2.8 в виде последовательности «кадров», сделанных с интервалом в одну двенадцатую цикла. То есть струна достигает состояния (g) через половину цикла после высвобождения из состояния (a). В течение второй половины цикла струна возвращается по этим шагам обратно в состояние (a), и так далее, до бесконечности. Судя по всему, немногие гитаристы знают, что струна колеблется таким антисимметричным образом, когда перемещение идет по диагонали7. Из этого факта следуют некоторые очень важные выводы, которые будут изложены в Главе 4.
Хотя начальная стадия движения настоящей струны будет похожа на изображенное на Рис. 2.8 (разумеется без резких переломов), струна никогда не вернется точно в первоначальное положение, поскольку она сразу же начнет терять энергию. Это происходит в основном тремя способами.
(a) Взаимодействие с верхней декой
Идеальная струна, жестко зафиксированная в каждом конце, не может отдавать энергию своих колебаний. Жесткие опоры действуют как идеальные отражатели для любой волны, подходящей к ним вдоль струны, и таким образом неопределенно долго поддерживают колебания, сами при этом оставаясь неподвижными. В первом приближении в качестве таких препятствий работают верхний порожек (или лад) и косточка гитары … если бы это было не так, то колебания струны гасились бы мгновенно. Однако верхняя дека, несмотря на то, что она усилена планками и подставкой, имеет некоторую гибкость. Она слегка поддается под действием периодического усилия, которое передается от колеблющейся струны через подставку, и таким образом энергия от струны постепенно передается верхней деке, которая в свою очередь излучает часть этой энергии в виде звуковых волн. Более тяжелые струны возбуждают верхнюю деку сильнее, чем легкие, но, таким образом, отдают свою энергию быстрее.
Рис. 2.8 Движение идеальной струны после высвобождения
Хотя это довольно простой принцип, детали взаимодействия струны и верхней деки могут быть очень сложными. Мы не будем пытаться их все учесть, поскольку они в большей степени являются проблемами изготовителя инструмента, а не исполнителя. Но тот факт, что гитарист может управлять долей энергии струны, которая будет передана верхней деке, а не рассеяна другими способами, непосредственно относится к теме книги, причем в такой степени, что он послужил основой следующей главы и является одной из главных идей этой книги.
(b) Внутреннее демпфирование
Повторяющиеся деформации струны во время колебаний вызывают внутреннее трение. Мера рассеяния энергии таким способом зависит от материала струны. В сплошных металлических струнах этот эффект обычно пренебрежимо мал, но в нейлоновых струнах он, возможно, является главным механизмом демпфирования. Скорость потери энергии в материале увеличивается с ростом частоты, что приводит к тому, что в материалах с высоким внутренним демпфированием высшие формы колебаний затухают быстрее, чем низшие. Очень быстрое затухание высших форм колебаний обуславливает более мягкий по сравнению со стальными струнами звук нейлона, а также глухой и безжизненный звук басовых струн, которые требуют замены, или, по крайней мере, чистки. (Предположительно в этом виноваты влага и жир с пальцев, которые постоянно проникают через обмотку в нейлоновый сердечник, что постепенно увеличивает внутреннее демпфирование басовой струны.) По этой же причине при внимательном прослушивании ноты, взятой близко к подставке на одной из нейлоновых дискантных струн, обнаруживается что острая, металлическая окраска звука присутствует только в самом начале: спустя долю секунды большая часть яркости уйдет.
(c) Демпфирование воздухом
Третий по важности способ, которым колеблющаяся струна теряет энергию, заключается в преодолении сопротивления воздуха. Скорость потери энергии также увеличивается с ростом частоты, но не так быстро, как в случае внутреннего демпфирования. Кроме того, эта скорость для тонких, легких струн выше, чем для более толстых и тяжелых. Это может быть одной из причин того, что одна и та же нота будет звучать дольше на одной струне, чем на другой. Например, нота Ми (330 Гц) вполне может прозвучать в три раза дольше, если ее извлечь как флажолет на пятой или шестой струне, чем если ее извлечь на открытой первой струне, которая легче и тоньше всех остальных. Однако внутренне демпфирование также играет здесь роль, и в общем случае для нейлоновых струн оно более важно, чем демпфирование воздухом.
Из трех описанных способов потери энергии к появлению звука приводит только взаимодействие с верхней декой. Можно подумать, что два других способа являются бессмысленными тратами энергии, но если бы это было так, то тогда не было бы смысла использовать нейлоновые струны вместо стальных. Внутреннее демпфирование нейлона выборочно, оно приводит к более быстрому затуханию высших форм колебаний. Это выборочное демпфирование является важнейшей особенностью звучания классической гитары. В следующем разделе мы увидим, что гитарист может сам добавлять выборочное демпфирование.
2.10 Две техники выборочного демпфирования
(а) Пиццикато
Если поставить правую руку так, чтобы ребро ладони касалось струн вблизи подставки, то мягкая плоть будет поглощать небольшую часть энергии струны на каждом цикле ее колебаний. Это увеличивает степень демпфирования для всех форм колебаний, но высшие формы, которые имеют петлю вблизи подставки, подавляются особенно сильно. Это дает приглушенный, «шерстяной» звук с характерным «стуком», обусловленным малой длительностью каждой ноты.
Можно изменять степень демпфирования … сильное или умеренное, и положение точки, в которой оно выполняется. (Пухоль8 выделял четыре различных типа пиццикато, включая довольно забавное пиццикато эстриденте, при котором струну заставляют дребезжать об мякоть пальца, слегка демпфируя на значительном расстоянии от подставки.) Как вариант, струну можно демпфировать на другом конце, поставив палец левой руки непосредственно на порожек лада, а не за ним, как обычно. Сор9 рекомендовал использовать этот метод, хотя он и требует очень точной постановки пальцев и не дает такого разнообразия звуков. Его можно использовать, если правая рука слишком занята, чтобы менять позицию на необходимую для пиццикато, но в таких случаях столь же эффективно будет «поддельное» пиццикато, когда нота извлекается мясистой частью большого пальца (чтобы подавить высшие формы колебаний) после чего палец быстро возвращается на струну (чтобы остановить звучание ноты).
По мере увеличения степени демпфирования становится все сложнее различить высоту ноты, и, вообще-то, пиццикато является хорошим примером того, как гитарист может управлять чистотой звука. Хотя разные люди, несомненно, понимают это слово по разному, чистота в равной степени включает в себя яркость, четкую атаку и ясно различимую высоту. Звуку пиццикато недостает чистоты по всем трем параметрам. И наоборот, когда требуется получить чистый звук, можно различными способами подчеркнуть эти три качества. Кристальная чистота трудно достижима, и поэтому высоко ценится, но она не всегда нужна. Принцип разнообразия применим здесь точно также, как и к другим аспектам качества звука, и, изменяя чистоту звука, гитарист может добавить светотени к музыке, которую он исполняет.
(b) Флажолеты
Мы узнали, что демпфирование мякотью пальца близко к одному из концов струны будет поглощать энергию колебаний только постепенно, потому что в этих местах амплитуда колебаний очень мала. Если палец поставить в любом другом месте, то чаще всего колебания сразу же совсем прекратятся. Однако существуют особые точки на струне, в которых легкое демпфирование кончиком пальца даст не тишину, а новую, более высокую, ноту. Эти точки расположены на расстояниях, составляющих простую дробь от длины струны.
Представим, что мы дотрагиваемся до колеблющейся струны точно в ее центре. Все формы колебаний с нечетными номерами, включая основную, быстро заглушатся, поскольку в середине струны у них находится петля (точка максимальной амплитуды). Однако все формы колебаний с четными номерами, каждая из которых в этой точке имеет узел (то есть неподвижную точку), продолжают звучать практически неизменными. Если основная частота была равна f1, то оставшиеся формы колебаний будут иметь частоты в 2, 4, 6, 8 и т.д. раз большие f1 или, другими словами в 1, 2, 3, 4 раза большие чем 2f1. Следовательно, оставшийся звук воспринимается как новая нота с основной частотой 2f1 … на октаву выше первоначальной высоты.
Аналогично, прикосновение к струне на расстоянии в одну треть длины (от любого конца) заглушит все формы колебаний, за исключением третьей, шестой, девятой и т.д. Получившаяся нота будет иметь частоту 3f1, на октаву и квинту выше первоначальной. Прикосновение на расстоянии ровно в одну четверть длины даст новую основную частоту 4f1, на две октавы выше, и так далее.
Разумеется, обычная техника исполнения флажолетов (гармоник) заключается в том, что палец уже стоит на струне в момент защипывания. Палец, касающийся струны, мгновенно гасит ненужные формы колебаний, и дальнейшее его удерживание на струне после того, как флажолет зазвучит, не имеет смысла. Действительно, если продолжать удерживать палец на струне, то он начнет демпфировать сам флажолет, поскольку невозможно качаться струны, не оказывая на нее никакого давления, а любое давление, даже приложенное точно в узловой точке, будет нарушать свободные колебания струны. Таким образом, чтобы получить чистый звук флажолета, необходимо чтобы палец очень легко касался струны, а не давил на нее, и покидал струну сразу же, как струна будет защипнута.
Так называемые натуральные флажолеты исполняются на открытых струнах, когда палец левой руки касается струны, а палец правой руки защипывает ее. В этом случае середина струны расположена точно над двенадцатым ладом, седьмой и девятнадцатый лады лежат почти точно на одной трети длины струны от соответствующего конца, а пятый лад лежит на четверти длины. Это единственные лады, которые расположены на точных дробных расстояниях между верхним порожком и косточкой. Флажолет «на четвертом ладу» на самом деле извлекается в точке расположенной примерно на 4 мм ближе к верхнему порожку, чем четвертый лад, поскольку именно это расстояние равно одной пятой длины струны. Этот же флажолет можно извлечь в точке, отстоящей на расстояние в две пятых длины, которая расположена примерно на 4 мм ниже девятого лада, и на расстоянии в три пятых длины, чуть ниже шестнадцатого лада. Высоты натуральных флажолетов, разумеется, совпадают с частотами, соответствующими формам колебаний струны, приведенным на Рис. 2.2 для пятой струны.
Громкость флажолета зависит от выбранной точки защипывания. Совершенно не имеет смысла касаться струны в одной узловой точке, защипывая ее в другой узловой точке, однако именно это происходит, если, например, пытаться извлечь флажолет на седьмом ладу, защипывая над девятнадцатым. Чтобы в данном случае получить громкий флажолет, необходимо защипывать на расстоянии от подставки не превышающем одну шестую длины струны. Точка защипывания для флажолета на девятом ладу должна быть еще ближе к подставке, на расстоянии, не превышающем одну восьмую (примерно 7.62 см от подставки). Вообще говоря, если вы хотите получить сильный и чистый звук, то чем выше флажолет, тем ближе точка защипывания должна быть расположена к подставке. Поэтому так называемые искусственные флажолеты, которые исполняются на струнах, прижатых на каком-либо ладу, правой рукой, которая одновременно и касается струны (указательным пальцем), и извлекает звук (безымянным или большим), звучат слабее. Кончик указательного пальца должен находиться в середине струны, на двенадцать ладов выше лада, на котором прижата струна, и поэтому точка защипывания не может находиться близко к подставке.
Эффект, который расположение точки защипывания оказывает на качество флажолета можно показать, снова рассмотрев натуральный флажолет на двенадцатом ладу. В этом случае самой низкой из присутствующих форм колебаний будет вторая, которая сильнее всего возбуждается при защипывании в p = 1/4 (см. раздел 2.6), однако две следующих формы, четвертая и шестая, лучше всего возбуждаются при защипывании в точках p = 1/8 и p = 1/12, соответственно. Защипывание флажолета в точке p = 1/4 фактически даст такой же звук, как и защипывание открытой струны в середине. Чтобы флажолет имел такую же «изюминку», как и открытая струна, защипнутая в обычной позиции, точка защипывания должна находиться значительно ближе к подставке, примерно в p = 1/10.
То же самое можно сказать и в отношении движения защипывания, подходящего для флажолета. Чем выше флажолет, тем меньше смысла в постепенном высвобождении струны, поскольку тогда подавляются высшие формы колебаний (см. раздел 2.8). Таким образом, чтобы получить яркий звук флажолета на пятом ладу, который содержит только формы колебаний с номерами 4, 8, 12, 16, 20 и так далее, необходимо использовать ноготь скорее в качестве медиатора, чем пандуса, и он должен быстро проходить через струну.
2.11 Эффект жесткости струны
Мы уже упоминали о том, что жесткость струны препятствует ее изгибу под острым углом и тем самым ограничивает количество форм, по которым можно заставить колебаться струну. Сейчас читатель может выполнить следующую грубую проверку, позволяющую определить наивысшую форму колебаний, слышимую на каждой струне.
Метод заключается в извлечении флажолетов, касаясь струны не мякотью кончика пальца, а более узким, но не слишком плотным объектом (я применяю ребро стирательной резинки), и защипывая струну возле подставки острым медиатором или уголком ногтя. Таким образом, можно заставить достаточно четко звучать флажолеты, намного более высокие, чем извлекаемые обычным способом. По мере приближения демпфирующего объекта к концу струны (в этом случае наиболее удобным будет конец на подставке), номера гармоник и их количество возрастают, а их громкость слабеет. В результате мы придем в такую точку, в которой невозможно будет извлечь дальнейшие гармоники, а будет слышен только шум. Если теперь отвести демпфер назад к точке, в которой будет слабо слышен четко выраженный музыкальный звук, то эту точку можно считать первым узлом наивысшей действующей формы колебаний. Определить номер этой формы можно, просто поделив длину струны на расстояние между узлом и косточкой.
Нейлоновые струны без обмотки на моей гитаре дают наивысшую различимую форму колебаний в начале третьего десятка (25 на первой, 22 на третьей). Для басовых струн с металлической обмоткой это число выше, в пределах от 31 для четвертой до 39 для шестой. Я не гарантирую точности этих значений, а привожу их лишь в качестве приблизительных. Наивысшие гармоники на дискантных струнах очень трудно отличить от шума защипывания струны, поскольку их частоты очень высоки (примерно до 8000 Гц на первой струне) и они очень быстро затухают. Тем не менее, теперь мы имеем представление о длине наименьшего отрезка струны, на котором могут совершаться колебания. Например на первой струне длина наименьшего отрезка составляет около дюйма (25.4 мм); это означает что, с точки зрения музыкального звука, мы не получим никаких изменений, если будем защипывать струну на расстоянии от косточки меньшем, чем половина дюйма.
Не следует ожидать, что длина наименьшего отрезка струны, прижатой на каком-либо ладу, уменьшиться по сравнению с открытой. Из этого следует, что число действующих форм колебания струны уменьшается с ростом номера лада, на котором она прижата. Таким образом, если нота, извлеченная на открытой струне, имеет 22 различимых обертона, то нота на той же струне, прижатой на двенадцатом ладу, будет иметь только 11 различимых обертонов. Это в некоторой степени объясняет, почему одна и та же нота может иметь разный характер, если ее извлечь на разных струнах. Например, Ми (330 Гц), если ее извлечь на первой открытой струне, может содержать 25 обертонов, но эта же нота, извлеченная на третьей струне (на девятом ладу) будет содержать примерно вполовину меньше обертонов, что придаст ей более темный и густой характер. С другой стороны, эта же нота, извлеченная на четвертой струне (на четырнадцатом ладу) будет содержать примерно столько же обертонов, что и нота, извлеченная на третьей струне, но при этом будет звучать сильнее и ярче, особенно если струна новая. Однако этот парадокс разрешится, если учесть процессы потери энергии, описанные в разделе 2.9. Новая четвертая струна не подвержена действию сильного внутреннего демпфирования нейлона, которое подавляет высшие формы колебаний, как на третьей, а поскольку она тяжелее, она сильнее возбуждает верхнюю деку.
На звук ноты, сыгранной на разных струнах, влияют еще несколько факторов. Например, при перемещении левой руки вверх по грифу гитаристы часто не изменяют положение правой руки пропорционально левой, смещая, таким образом, точку защипывания ближе к середине струны. Кроме того, чем выше номер лада, тем легче становится выполнять вибрато; а, например, третья струна в общем более чувствительна к вибрато, чем первая или четвертая, потому что ее натяжение значительно слабее.
Все эти факторы, а также и другие, относящие к отклику инструмента, и которые будут рассмотрены в следующей главе, в своей совокупности придают каждой ноте гитары свою собственную окраску и диапазон возможностей. Чем внимательнее мы прислушиваемся, тем большее разнообразие мы можем обнаружить, не только между разными нотами, но и в пределах звучания отдельной ноты. Гитарист, восприимчивый к этому разнообразию, и знающий, как использовать окраску в качестве неотъемлемой части исполнения, может превратить даже простейшую пьесу в захватывающее переживание. Но такая магия не рождается по мановению волшебной палочки, для нее необходима прочная база технического контроля, и именно здесь знание основных принципов может стать очень ценным инструментом.
|





